Основа поверхностной модели – поверхности и кривые NURBS.
Чтобы быстро и легко нам разобраться в этой удивительной программе, и в дальнейшем разговаривать на «одном языке», я расскажу об основных понятиях и терминах, которые будут использоваться нами в следующих статьях и уроках. А начну я с основы основ любой программы поверхностного проектирования – с поверхностей (Surface) и кривых (Curve). А точнее, именно с кривых – ведь любую поверхность можно представить их бесконечным множеством.
Итак, кривые…. Как кривые описываются в программе? Какие бывают кривые, какими свойствами они обладают? На эти вопросы я и постараюсь ответить. Хочется рассказать о них как можно проще, без нудных математических выкладок. Как получится – не знаю, но всё равно попробую.
А что такое собственно сама кривая? Это, как видится мне, изогнутая в пространстве линия (проволочка, волосок и т.д.) нулевой толщины. Известно, что любую линию (и даже изогнутую), мы можем представить в виде сегментов различной длины, состоящих из прямых линий (прямых). Получается, что она может быть описана множеством простых уравнений описания прямых, известных нам из геометрии. Вроде всё просто! Но при более детальном рассмотрении такого способа определения кривой, становятся очевидными и очень весомые недостатки:
- Невозможность масштабирования такой кривой – при увеличении сразу становится видна её «угловатость».
- Форма объекта, аппроксимированная линейными сегментами, может изменяться при некоторых преобразованиях (например – вращении).
- Для более или менее достоверной аппроксимации требуется огромное количество линейных сегментов.
Указанные недостатки заставляют искать другие способы описания кривых. В 1885 году Карл Вейерштрасс сформулировал и доказал теорему, из которой следует, что любую кривую можно нарисовать с помощью полиномов. Что такое полином (многочлен), как я думаю, Вы знаете из школьного курса алгебры, напомню только, что для одной переменной x он имеет следующий вид:
y = a0xn +a1xn-1...+an,
где а — коэффициенты многочлена, п — показатели степеней (целые неотрицательные числа).Вопросом о построении аппроксимирующего многочлена занимались многие учёные. Среди них главную роль сыграл Сергей Натанович Бернштейн, который вывел необходимый полином. А применил на практике, впервые в компьютерной графике, французский инженер компании "Рено" Пьер Безье. Теперь каждый человек, занимающийся компьютерной графикой, знает что такое "кривая Безье" и "инструменты Безье".
Всё выше сказанное относится к определению кривой в пространстве в явном виде, то есть когда определённому значению х соответствует одно значение y и z. Примеры таких кривых нам известны из школьного курса алгебры. Это – прямые, синусоиды, параболы и т.д. Этот способ позволяет легко и быстро строить графики, но обладает рядом существенных недостатков:
- Так как каждому значению х соответствует одно значение у (и z), то невозможно начать новый фрагмент кривой в произвольном месте.
- Такая кривая не может быть замкнутой (конец кривой совпадает с её началом).
В результате явный способ представления не может применяться там, где требуется описание произвольных кривых, размещаемых в различных местах на плоскости.
Далее великая конструкторская мысль привела учёных к иному способу описания кривых – с помощью параметрических выражений. Особенностью этих функций является то, что координаты точки кривой x, y и z равноправны, то есть они вычисляются каждая отдельно в зависимости от некоторого параметра t. Такое определение кривой назовём параметрическим. В общем виде параметрическую функцию Q(t) можно записать в следующем виде:
Q(t)={ X(t), Y(t), Z(t)}.
Для примера в качестве параметра t можно принять значение времени (хотя на практике это не обязательно), и представить, как некоторая частица будет двигаться по кривой в некотором промежутке времени. В начальный момент (t=0) частица будет находиться в начале кривой, а при t=1 – в конце. Соответственно, при некотором значении t, лежащем от 0 до 1, частица будет иметь вполне определённые значения координат x,y, и z. При этих значениях параметра t (от 0 до 1) параметрическая функция будет называться нормализованной.
Второй особенностью параметрической функции является то, что она позволяет получить более разнообразные формы кривых, чем выражения, задающие форму кривой явно. Применение параметрических функций позволяет применять более сложные функции, а не только линейную аппроксимацию, так как одним из основных недостатков аппроксимации прямыми является, как уже отмечалось выше, наличие угловых изгибов, которые даже при небольшом увеличении создают впечатление ломаной линии, то есть на кривой будут заметны перегибы.
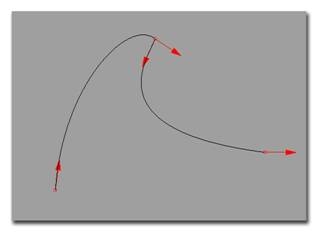
Перегиб (Kink) – это точка на кривой, где кривая резко изменяет свое направление. Например, углы прямоугольника — это точки перегиба. Точки перегиба также находятся там, где кривая резко изменяет величину своей кривизны. Например, скругленный прямоугольник имеет точки перегиба там, где линейные отрезки переходят в дуги. На рисунке мы видим точки перегиба (красного цвета) на различных кривых.
 |
Точки перегибов на различных кривых. |
Отсутствие точек перегиба на кривой будет говорить о её гладкости. Гладкость так же означает, что при моделировании на кривой не образуется петель и разрывов. Но при этом, не исключена возможность создания, как гладкого сопряжения, так и изгибов, например острых углов. Хорошим примером гладкой замкнутой кривой, с достаточно острым преломлением, является кривая, повторяющая аэродинамический профиль крыла. Если рассматривать движущую частичку по кривой, то можно сказать, что в случае гладкой кривой, эта частица на своём пути не должна будет останавливаться и резко менять своё направление движения.
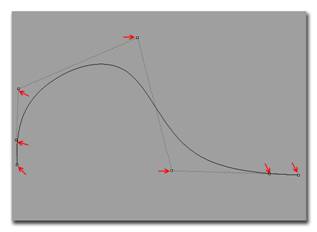
А теперь, давайте укрепим на частице стрелку, которая будет указывать направление движения, и назовём её касательной к кривой, в том месте, где на данный момент будет находиться наша частичка. Если касательная, в каждой точке кривой будет иметь одно направление, то такая кривая будет гладкой, а если два, то – нет. На рисунке слева изображена гладкая кривая, а справа – с изломом.
 |
|
Гладкая (слева) и с изломом (справа) кривая. |
|
Хочется сказать, что именно гладкие кривые получили наибольшее распространение при моделировании различных объектов. Почему, я думаю, Вам будет понятно, если Вы посмотрите на формы современных автомобилей, самолётов, различной бытовой техники и биологических объектов. Для построения аналогичных моделей объектов, в компьютерной графике, используются гладкие NURBS - кривые и поверхности, описываемые параметрическими функциями, и которые обладают рядом "положительных" свойств. Ниже я рассмотрю свойства NURBS-объектов на примере кривых. Но всё сказанное, как говорилось выше, будет относиться и для поверхностей, ведь всегда можно представить поверхность набором ортогональных кривых, задающих свойства поверхностей в двух направлениях (u и v). Кривые NURBS ещё называют сплайнами (splines).
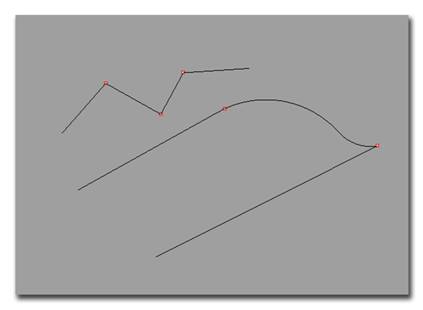
Понятие сплайна пришло к нам ещё с тех времён, когда компьютеров не было и в помине. Все линии чертежа конструктора рисовали вручную по линейке и с помощью других, простейших инструментов. Для создания гладких, изогнутых линий в натуральную величину (например, при строительстве кораблей) применялись длинные гибкие полосы дерева или металла. Для того чтобы придать упругой полоске нужную форму, ее фиксировали в требуемых точках с помощью особых свинцовых грузил, которые за сходство формы назывались "утятами". Результирующая кривая получалась гладкой, а форма изменялась перемещением грузил в плоскости чертежа. Компьютерный сплайн строится аналогичным образом: изначально прямолинейная кривая подтягивается к контрольным точкам (КT) (грузам), и получается изогнутая, гладкая линия. Каждая контрольная точка воздействует не на всю кривую целиком, а только на её некоторую часть. При чём величина "притяжения" кривой к точке (грузу) будет разной, что приведёт к различной степени изгиба. На рисунке ниже мы можем увидетья построение сплайна. Справа мы можем видеть изгибание гибкой рейки путём притягивания её к грузам, а справа – компьютерное построение сплайна.
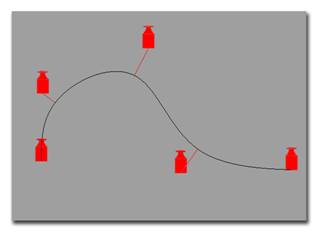 |
|
Построение сплайна (красными стрелками показаны контрольные точки). |
|
Один из наиболее простых способов изменить геометрию NURBS кривой - это переместить ее контрольные точки. Rhino предоставляет несколько способов перемещения контрольных точек. Для того, чтобы значительно переместить контрольную точку в произвольном направлении, нам просто надо перетащить её мышкой. Rhino также имеет инструменты, предназначенные для небольших, точных перемещений.
Любая кривая будет определяться степенью (n) (degree), которая является целым положительным числом (например: 1,2,3 и т.д.). Линии и ломаные линии в Rhino имеют степень, равную 1, окружности имеют степень равную 2, а большинство кривых сложной формы имеют степень 3 или 5. Rhino позволяет нам работать с кривыми от 1 до 11 степени. В некоторых случаях используются понятия линейной, квадратичной и кубической кривой.
Мы также можем столкнуться с понятием порядка (order) NURBS-кривой. Порядок NURBS-кривой — это положительное целое число на 1 большее её степени. Увеличение степени кривой не приведёт к изменению её формы, а обратноё преобразование изменит её.
Минимальный набор контрольных точек (КTmin) любой кривой будет определяться следующим выражением:
КTmin=n+1.
А теперь давайте представим частицу, летящую в космическом пространстве, по траектории некоторой кривой. На траекторию её движения будут оказывать влияние другие космические тела (контрольные точки). Причём воздействовать они будут на частицу одновременно, когда она будет пролетать через область их влияния, но с разной силой. Значение этой силы будет определяться размерами космических тел (сила гравитации) и их удалённостью от неё. Сначала допустим, что сила гравитации всех тел будет равна. Можно сказать, что каждое космическое тело (контрольная точка) будет максимально воздействовать на частицу лишь в определённой точке пространства, а при удалении от неё она сила этого воздействия будет ослабевать. Если нарисовать график этого воздействия от параметра t, то он примет форму колокола. Таким же образом будут воздействовать на частицу и другие тела (контрольные точки). Эту зависимость можно представить графически в виде "В-сплайна", который является базовой функцией контрольной точки, и определяет последние две буквы термина NURBS.
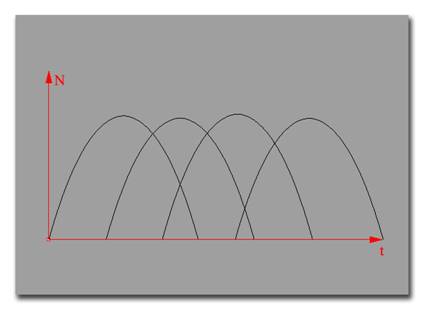 |
Базовые функции четырёх контрольных точек. |
На какие участки кривой будут воздействовать базовые функции контрольных точек? Чтобы определить это, весь диапазон параметра t мы разобьем на куски, а числа, определяющие эту разбивку, назовём узлами (knots). Множество узлов назовём узловым вектором. В этом случае под словом "вектор" понимается не направление в пространстве, а именно простой набор чисел. Если значения в наборе разделены одинаковым промежутком, то такие узлы называются однородными. В противном случае узлы будут неоднородными (см. рисунок ниже). Буквы NU в аббревиатуре NURBS означают как раз неоднородность (non uniform) и показывают, что узлы в NURBS-кривой могут быть неоднородными.
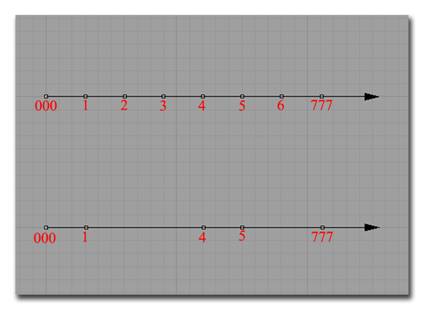 |
Сверху изображён однородный узловой вектор, а справа – неоднородный. |
Узлы могут иметь различную кратность. Она определяется количеством одинаковых чисел. Кратность узла не может быть выше степени кривой, и если она равна ей, то такие узлы будут называться полнократными. На рисунке видно, что узловые вектора начинаются и заканчиваются полнократными узлами. Кратность узлов в середине вектора делает кривую менее гладкой. Наличие полнократного узла говорит о том, что кривая может иметь острый перегиб. Таким образом, удалением и добавлением узлов можно управлять гладкостью кривой. Для этого в Rhino есть соответствующие инструменты. Количество узлов (U) связано с количеством контрольных точек (КT) и степенью кривой (n) следующей зависимостью:
U=KT+n-1.
Частое заблуждение — это то, что каждому узлу соответствует одна контрольная точка. Это верно только для NURBS кривых первой степени (ломаных). Для NURBS кривых бо'льших степеней существуют группы, количество узлов в которых вычисляется по формуле:
Ug=2*n.
Количество контрольных точек, соответствующих группе узлов будет равно:
KTg=n+1.
Например, возьмем NURBS кривую третьей степени с семью контрольными точками и узлами 0,0,0,1,2,5,8,8,8. Первые четыре контрольные точки сгруппированы в набор с шестью узлами - 0,0,0,1,2,5. Контрольные точки со второй по пятую сгруппированы в набор с узлами 0,0,1,2,5,8. Контрольные точки с третьей по шестую сгруппированы в набор с узлами 0,1,2,5,8,8. Последние четыре контрольные точки сгруппированы в набор с шестью последними узлами. О чём это говорит? А это говорит о том, что всё количество контрольных точек будет разбито на группы, которые оказывают влияние только на те части кривой, которые соответствуют определённым группам узлов.
А теперь давайте добавим нашим небесным телам (контрольным точкам) вес (w), причём всем разный. Что произойдёт? Очевидно то, что траектория частицы сильнее отклонится к телам с наибольшим весом, хотя её форма будет напоминать предыдущую. Такой же вес есть и у каждой контрольной точки. Важно заметить, что существенным является только относительное изменение весов контрольных точек. Если вдвое увеличить веса всех контрольных точек, то форма кривой не изменится.
За некоторым исключением, значения весов точек всегда положительны. Когда все контрольные точки кривой имеют одинаковый вес (обычно 1), то такая кривая называется нерациональной, в противном случае такая кривая будет называться рациональной. Буква R в аббревиатуре NURBS означает как раз "рациональный" и показывает, что NURBS кривая имеет возможность быть рациональной.Некоторые NURBS-кривые, например, окружности и эллипсы, всегда будут рациональными.
Rhino предоставляет инструменты для оценки и изменения веса точек, и можно сказать, что каждая контрольная точка представляется четырьмя координатами {х, у, z, w}.
Для чего я, так достаточно подробно, рассказал о NURBS-кривых? Дело всё в том, что в Rhino существуют специальные инструменты редактирования, которые позволяют изменять все основные характеристики кривой, а также строить её по заданным характеристикам. И чтобы правильно работать с этими инструментами, необходимо знать определения и взаимосвязи этих характеристик.
Кривая Безье — это частный случай В-сплайнов (NURBS-кривых). Прикладное значение этих кривых рассмотрим чуть ниже, в разделе посвященному их построению. Команда HandleCurve иллюстрирует построение кривых Безье, и как раз позволяет нарисовать кривую так, как она создаётся во многих графических редакторах.
Хочется отметить, что наряду с контрольными точками, на кривой существуют точки редактирования, расположенные в тех местах, которые определяются усреднёнными значениями узлов. С помощью этих точек, как и с помощью контрольных точек, мы также можем влиять на форму кривой.